探秘并查集——数据世界的“社交圈”
今天来介绍下数据结构中,另一位“人物”——并查集。
场景引入:
比如某学校某专业,全国一共招收10人
那么广东招4人、北京招3人、浙江招3人。
那么这几个人呢,来自各个省/市的不同地方,但是他们都互不相识。
现在对这些人进行编号:0,1,2,3,4,5,,6,7,8,9
然后我们用数组对这个小组成员表示下
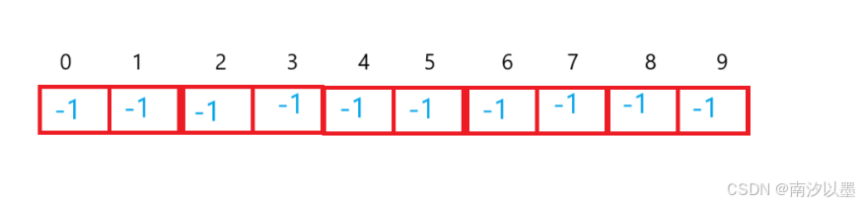
(负数稍后解释~)
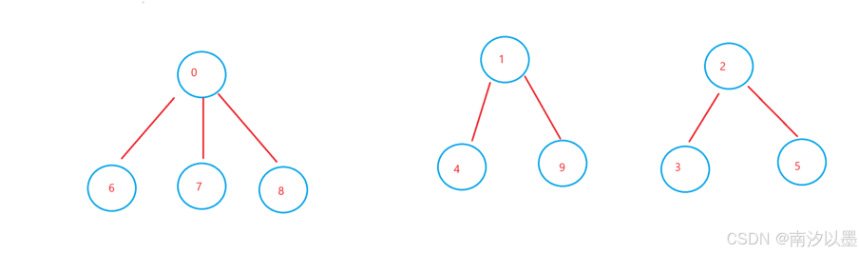
那么,到了出发去学校的日子,此时,三个地方组成三个小分队,即三个小集合
广东学生小分队:0,6,7,8
北京学生小分队:1,4,9
浙江学生小分队:2,3,5
此时分队里面是互相认识的,而且选了每个分队第一个学生作为队长,其树形关系可表示如下
那么对应数组呢,我们这样表示

此时呢,我们可以观察数组元素存放位置
可以得出这样的结论
1.数组编号对应集合中的编号
2.数组中元素值如若为负数,则代表根,数字本身代表整个树中有多少个元素
3.数组中元素值若不为负数,即说明,该值是父亲节点所在的下标值。
那么,即将到达学校之际,这时候呢,广东分队的6号同学和北京分队的1号同学认识了,并且相互介绍,此时呢,广东分队和北京分队的人都认识了,那么此时树形关系及其数组可表示如下: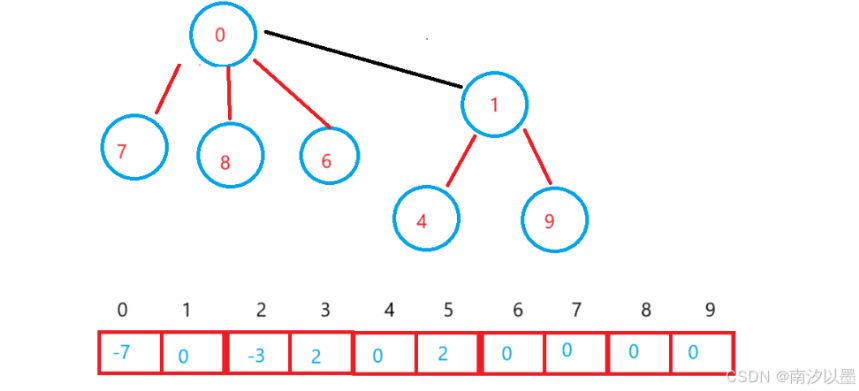
分析变化呢,得知
0下标:-4->-7
1下标:-3->0
4下标:1->0
9下标:1->0
合并后,其元素下标值需要做出相应的改变。
所以,通过以上方式进行存放后
利用这个,我们可以解决什么问题呢?
1.检查两个元素是否是在同一个集合中
2.检查元素值属于哪个集合
3.两个集合可以合并
4.集合的个数
那么,以上通过这个例子就粗略的介绍下了并查集
那么此时并查集的定义如下:
定义
:是一种数据结构,主要用于高效地处理一些不相交集合(Disjoint Sets)的合并及查询问题。它特别适合解决连通性问题,如检查元素是否属于同一个集合、图的连通分量。
那么接下来小编介绍下如何实现它吧
实现并查集
1.初始化
在这之前,我们通过这个场景引入,可以了解到,其底层是一个数组构成的,那么初始化的时候,其编号下标值设置为-1
那么我们就可以这样写
public class MyUnionFind {
//并查集底层是一个数组
public int [] elem;
public MyUnionFind(int n){
this.elem=new int[n];
Arrays.fill(elem,-1);
}
Arrays.fill()用于快速初始化和更新数组内容。
2.查找元素属于哪个集合
我们可以观察到,如若是树的孩子节点,那么此时,对应数组下标值是根节点的索引值
所以思路:按照数组数据元素生成的树,然后进行向上寻找,直到找到当前值为负数(根代表负数)
代码:
public int FindUnion(int n){
if(n<0){
throw new IndexOutOfBoundsException("数组下标不合法~");
}
while(elem[n]>=0){
n=elem[n];
}
return n;
}
值得注意的的是,我们查询的是孩子节点,即是大于0的值
3.判断两个元素是否是一个集合
思路:即判断两个元素所属的根是否在同一个集合中
代码:
public boolean isSameUnion(int x,int y){
int index1=FindUnion(x);
int index2=FindUnion(y);
if(index2==index1){
return true;
}else {
return false;
}
}
4.合并两个元素
思路:核心是要修改合并两个元素对应位置的数据,例:合并0和1两棵树,那么此时0下标的数值绝对值要变大,1的父亲边成了0
即对应的0下标元素值=0下标元素值+1下标元素值
1下标元素值=0下标
5码:
public void union(int x,int y){
int index1=FindUnion(x);
int index2=FindUnion(y);
if(index2==index1){
System.out.println("根相同,无法合并!");
return;
}else {
elem[index1]=elem[index2]+elem[index1];
elem[index2]=index1;
}
}
5.获取集合个数
思路就是遍历数组中有几个负数
这里思路简单直接上代码即可,
代码:
public int GetCount(){
int count=0;
for(int ret:elem){
if(ret<0){
count++;
}
}
return count;
}
值得注意的是没有人与自己连,自己就是自己的亲戚
源码:
public class MyUnionFind {
//并查集底层是一个数组
public int [] elem;
public MyUnionFind(int n){
this.elem=new int[n];
Arrays.fill(elem,-1);
}
/**
* 查找元素属于哪个集合
* 思路:按照数组数据元素生成的树,然后进行向上寻找,直到找到当前值为负数(根代表负数)
* @param n
* @return
*/
public int FindUnion(int n){
if(n<0){
throw new IndexOutOfBoundsException("数组下标不合法~");
}
while(elem[n]>=0){
n=elem[n];
}
return n;
}
/**
* 判断两个元素是否是一个集合
* 思路:即判读两个元素所属的根是否是同一个集合
* @param x
* @param y
* @return
*/
public boolean isSameUnion(int x,int y){
int index1=FindUnion(x);
int index2=FindUnion(y);
if(index2==index1){
return true;
}else {
return false;
}
}
/**
* 合并两个元素
* 思路:核心是要修改合并两个元素对应位置的数据,例:合并0和1,那么此时0下标的值要变大,1的父亲边成了0
* @param x
* @param y
*/
public void union(int x,int y){
int index1=FindUnion(x);
int index2=FindUnion(y);
if(index2==index1){
System.out.println("根相同,无法合并!");
return;
}else {
elem[index1]=elem[index2]+elem[index1];
elem[index2]=index1;
}
}
/**
* 获取根节点的个数,注意没有人与自己连,自己就是自己的亲戚
* @return
*/
public int GetCount(){
int count=0;
for(int ret:elem){
if(ret<0){
count++;
}
}
return count;
}
}
